The Muon Collider: Blurring Energy & Precision for New Physics Discovery

Table of Links

Abstract and 1. Introduction

2 Muons vs. Protons

2.1 Muon annihilation

2.2 Vector boson fusion

2.3 Annihilation vs. VBF

2.4 Signal vs. background

3 Muon Colliders Are Gauge Boson Colliders

3.1 From the effective vector approximation to PDFs

3.2 PDFs with broken electroweak symmetry

3.3 Impact of subleading logs

3.4 Finite mass effects

4 Physics

4.1 Electroweak symmetry breaking

4.2 Dark matter

4.3 Naturalness

5 Complementarity

5.1 EDMs

5.2 Flavor

5.3 Gravitational waves

6 Summary and Future Directions

Acknowledgments

A. Simplified Models

A.1 Standard Model

A.2 Supersymmetry

A.3 Vector-like quarks

A.4 Higgs portal

A.5 Hidden valleys

A.6 Axion-like particles

References

Abstract

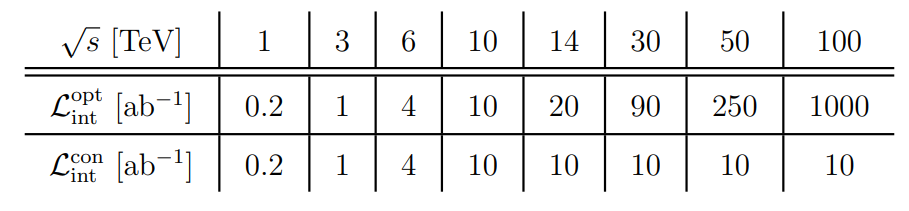
We lay out a comprehensive physics case for a future high-energy muon collider, exploring a range of collision energies (from 1 to 100 TeV) and luminosities. We highlight the advantages of such a collider over proposed alternatives. We show how one can leverage both the point-like nature of the muons themselves as well as the cloud of electroweak radiation that surrounds the beam to blur the dichotomy between energy and precision in the search for new physics. The physics case is buttressed by a range of studies with applications to electroweak symmetry breaking, dark matter, and the naturalness of the weak scale. Furthermore, we make sharp connections with complementary experiments that are probing new physics effects using electric dipole moments, flavor violation, and gravitational waves. An extensive appendix provides cross section predictions as a function of the center-of-mass energy for many canonical simplified models.

1 Introduction

The discovery of the Higgs boson [1, 2] at the Large Hadron Collider (LHC) marks the end of one era and the dawn of another. The origin of mass has been explained, but in answering this question, the Higgs boson poses a host of others: Is this the Higgs of the Standard Model? Is it the only Higgs, or one of many? Why is electroweak symmetry broken in the first place, and what sets the scale? How, if at all, is the origin of mass connected to the patterns of flavor, the nature of dark matter, or the abundance of matter over antimatter?

These questions make the call to explore shorter distances and higher energies as vibrant and clear as it has ever been. Although the path forward is devoid of guaranteed discoveries, the journey thus far has always been more a matter of serendipity than inevitability. We build colliders not to confirm what we already know, but to explore what we do not. In the wake of the Higgs boson’s discovery, the question is not whether to build another collider, but which collider to build.

Over the course of the last decade, consensus has largely coalesced around linear or circular e +e − colliders [3–6] and circular pp colliders [7, 8], both of which constitute natural extensions of past and present machines. The strengths of these two approaches are largely complementary, with the precision of e +e − machines and the power of pp machines paving distinct paths toward the exploration of physics at shorter distances. Loosely speaking, the strength of the former is to reveal the fingerprints that new physics has left on the properties of the Higgs and other electroweak states, while the latter are positioned to produce the new physics directly. This has given rise to a familiar dichotomy between energy and precision as contrasting approaches to search for new physics.

Enter the muon. The potential advantages of high-energy muon colliders have long been recognized [9–15]. As a fundamental particle, the muon’s full energy is available in a collision, with far cleaner final states relative to those produced by the dissociation of a composite particle like the proton. Its considerable mass suppresses the synchrotron radiation that effectively limits the energies of circular e +e − colliders, making both high energies and high luminosities achievable with a relatively small footprint. This raises the prospect that a muon collider could exceed the direct energy reach of the LHC, while achieving unprecedented precision measurements of Standard Model processes. The muon allows us to leverage the benefits of both energy and precision in a unified future collider program.

These advantages come at a cost: the colliding particles are no longer stable. The short lifetime of the muon imposes a series of technical challenges that must be overcome before such a collider can be realized. But progress towards this end has hastened considerably in recent years, spearheaded by the US Muon Accelerator Program (MAP) [16–19], the Muon Ionization Cooling Experiment (MICE) [20–22], and the Low Emittance Muon Accelerator (LEMMA) concept [23]. Developments on the accelerator side have catalyzed experimental and theoretical activity, reflected by input to the European Particle Physics Strategy Update [24] and the proliferation of studies outlining aspects of the theory case for muon colliders at various energies. Recent contributions include studies of the electroweak boson PDF of the muon [25]; the production of new scalars [26–31] and diverse other states [32] in vector boson fusion (VBF); the discovery potential for minimal dark matter [33, 34]; the measurement of the Higgs self-couplings [35] and couplings to electroweak bosons [36]; the sensitivity to new physics encoded in irrelevant operators [37, 38]; and the coverage of potential BSM explanations for hints from the complementary experiments yielding the muon g −2 [39–43], B meson [44], and K meson [45] anomalies.

In this paper, we present an aspirational theory case underlining the physics potential of a high-energy muon collider. We aim to identify energy and luminosity goals that would position such a collider as a natural successor to the LHC. Our approach synthesizes some of the qualitative lessons of earlier studies (e.g. [28,32,33]), identifies entirely new physics objectives, and explores complementarity with forthcoming experiments across various frontiers. We summarize qualitative features of the most important production modes and characterize the electroweak gauge boson content of the initial state for both Standard Model and beyond-theStandard Model final states; present a range of case studies demonstrating the muon collider’s potential to shed light on electroweak symmetry breaking, dark matter, and the naturalness of the weak scale; and sharpen connections to complementary experiments probing new physics through electric dipole moments (EDMs), flavor violation, and gravitational waves. Although our primary focus is on high-energy muon colliders, it bears emphasizing that many of the same physics considerations are applicable to other high-energy lepton colliders, and aspects of this work are relevant to the physics case for potential long-term upgrades of the ILC.

For the most part, the studies presented here involve rate measurements and an accounting of simple irreducible backgrounds. More detailed projections are necessarily subject to a host of experimental considerations, and future developments in accelerator, detector, and theory studies for a muon collider are closely intertwined. Muons at rest have a relatively short lifetime of 2.2 µs and, while the push to high momentum beams can extend

the lab frame lifetime up to the order of seconds, the exponential decay of the muon produces an intense source of collinear off-momentum electrons. The electrons then interact with the beamline components, producing electromagnetic showers that result in a high flux of low-energy photons and soft neutrons; these are the primary source of background for a muon collider detector. The process of bending and ultimately focusing the beams to generate a high luminosity collision rate directs these off-momentum backgrounds into collimators upstream and also very close to the interaction point. The exact share of these backgrounds depends strongly on the machine lattice and the interaction point configuration. In all cases, the incorporation of shielding cones close to the interaction point has been identified as significant means of mitigating the effects of beam-induced background inside the detector [46].

Detector studies performed in [47] show that the current approach to handle high detector backgrounds appears adequate to preserve the physics capabilities. These studies need to be extended and updated to incorporate recent breakthroughs in technology and higher center of mass energies. For backgrounds incident on the detector elements, the primary tool for separating collider events from beam-induced background (BIB) is the new generation of precision timing detectors, which leverage the large investment of effort going into HL-LHC upgrades [48,49]. In the context of the present work, we take this as an encouraging indication that beam-induced backgrounds and associated reconstruction issues can be addressed, but emphasize that all of the studies herein represent estimates in need of detailed experimental study.

As this study will articulate, there is abundant motivation to build a future muon collider. The technological challenges do not appear to be insurmountable, and provide a wealth of opportunity to develop new experimental techniques. The way the muon collider blurs the line between energy and precision opens the door to novel analysis approaches, while motivating new higher order calculations. And such a machine could readily furnish answers to many of the fundamental questions in particle physics.

The muon-smasher’s guide is organized as follows: In Sec. 2, we sketch many of the main qualitative features of collisions at high-energy muon colliders, with an eye towards their advantages over pp colliders and the interplay between various production modes. In Sec. 3, we turn to the physics of the initial state at high-energy muon colliders, characterizing the electroweak gauge boson content of high-energy muons and developing a pragmatic approach to capturing the most important effects. The broad physics case is developed in Sec. 4, focusing mainly on the central themes (electroweak symmetry breaking, dark matter, and naturalness) highlighted by the discovery of the Higgs. In Sec. 5, we explore the complementarity of a muon collider with other experiments operating on compatible timelines, with a particular focus on electric dipole moments, flavor violation, and gravitational waves. We summarize the central lessons of the study in Sec. 6, underlining the energies and luminosities that would position a muon collider to address the questions posed by the Higgs discovery. We reserve a compendium of cross sections and the details of various analyses for App. A.